2極を並列に接続したら電流は2倍に? (前編)

2極を並列に接続したら電流は2倍流せるのか?
たとえば、ここに 1極(1P)10Aの端子、コネクタ、接点などがあったとします。 いま20Aの電流を流したいけれど、20A流せるのものがなかったので この10Aのものを2極並列に接続して、20Aとして使おうと思いますが、、、 どうなのでしょうか?
単純に計算すれば数字上は 10A+10A=20Aとなり、【ОK】なのですが、 それで良いのでしょうか? このような足し算は成り立つのでしょうか? そのまま通り過ぎてしまいそうになりがちなのですが、まてよ、と疑問に思ったのでちょっとだけ考えてみたいと思います。 果たして正解は、、、
無機質な内容で退屈して眠くなるかもしれませんが、あまり難しく考えずに、優しく易しく、楽しみながらゆるーくゆっくりと進んでいきましょう!
まずは接点で考えてみましょう

ON-OFF
上で、端子、コネクタ、接点とありますが、ここでは代表として比較的ピンときやすい接点で、まずは考えてみたいと思います。 接点は何かと何かが接するところで、いろいろなものがありますが、ここでは数ある接点のうち、まずは簡単な電気の接点であるスイッチで考えてみることにしましょう。 一つの例としては、壁などに設置されパチパチと照明を点けたり消したりする、皆様おなじみのあのスイッチです。
彼と彼女の接点は?、、、それは筆者には理解不可能で、おそらくまったく別物ですので他の機会にでも考えていただければと思います。
さて、そのスイッチの内部で実際に電流を入り切りする心臓部的な部分の接点ですが、回路記号にすると一例として図【ON-OFF】のようなものです。
接点がON-OFFすると、、、
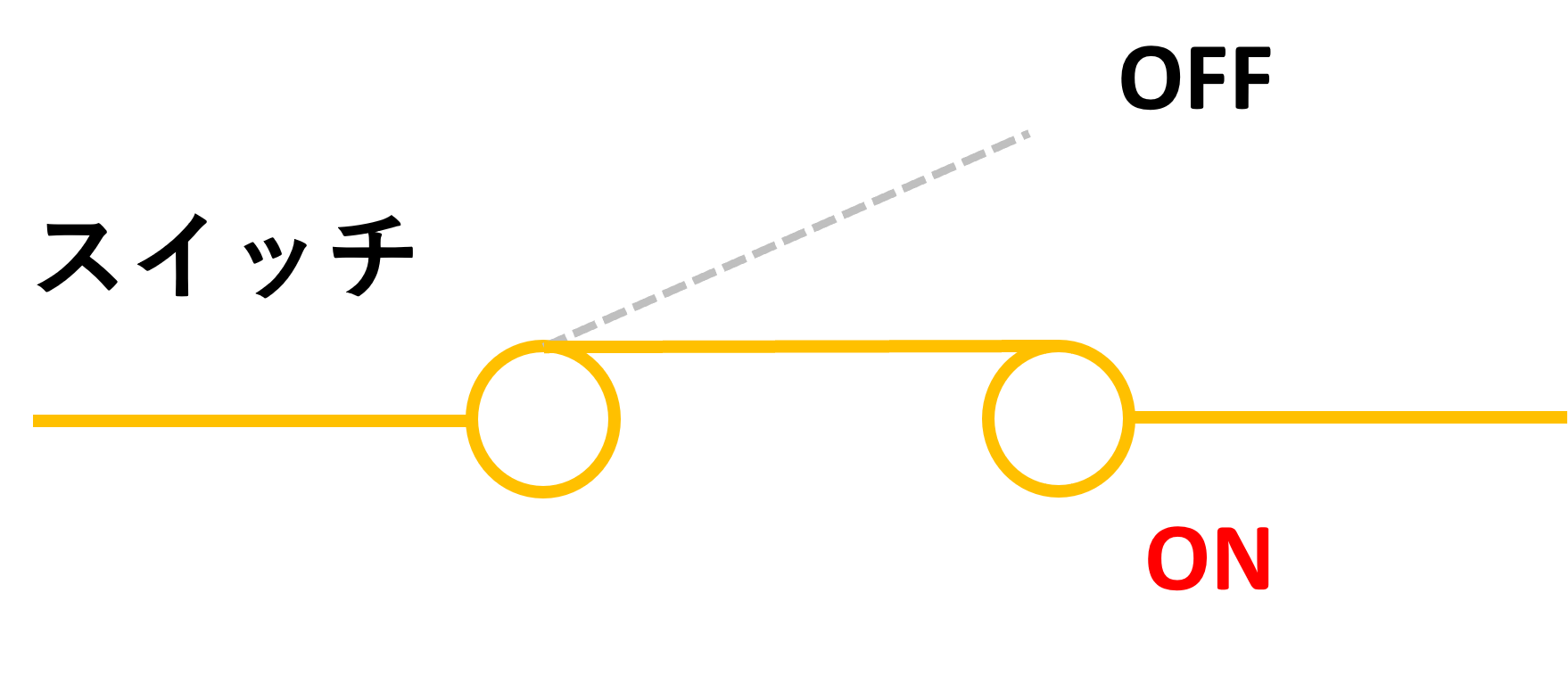
ON
二つの端子間で、金属片をシーソーのようにギッタンバッコン --- シーソースイッチの名称の由来(特にON-ONタイプの場合シーソーそっくりの動きになります。 ちなみに、狭い場所で、音楽を奏でてくれるスイッチは、スキマスイッチと言います --- これはUSOです。) --- と動かして電流をON-OFFしますが、通電中に、ON → OFFや、OFF → ONの切り替えを行ったときは、また別の要素が入ってきますので、ここではスイッチはONのままとし、入れたり切ったりはしないものとして考え、ON-OFFするという部分は後ほど考えることとします。 コネクタなどの接続器は電圧がかかった状態で接続したり、通電中に抜いたりすることが、スイッチのON-OFFと似たことになります。 まずは図【ON】のように、ON状態に固定して考えてみることにします。
ふつうは抵抗ゼロというわけにはいきません
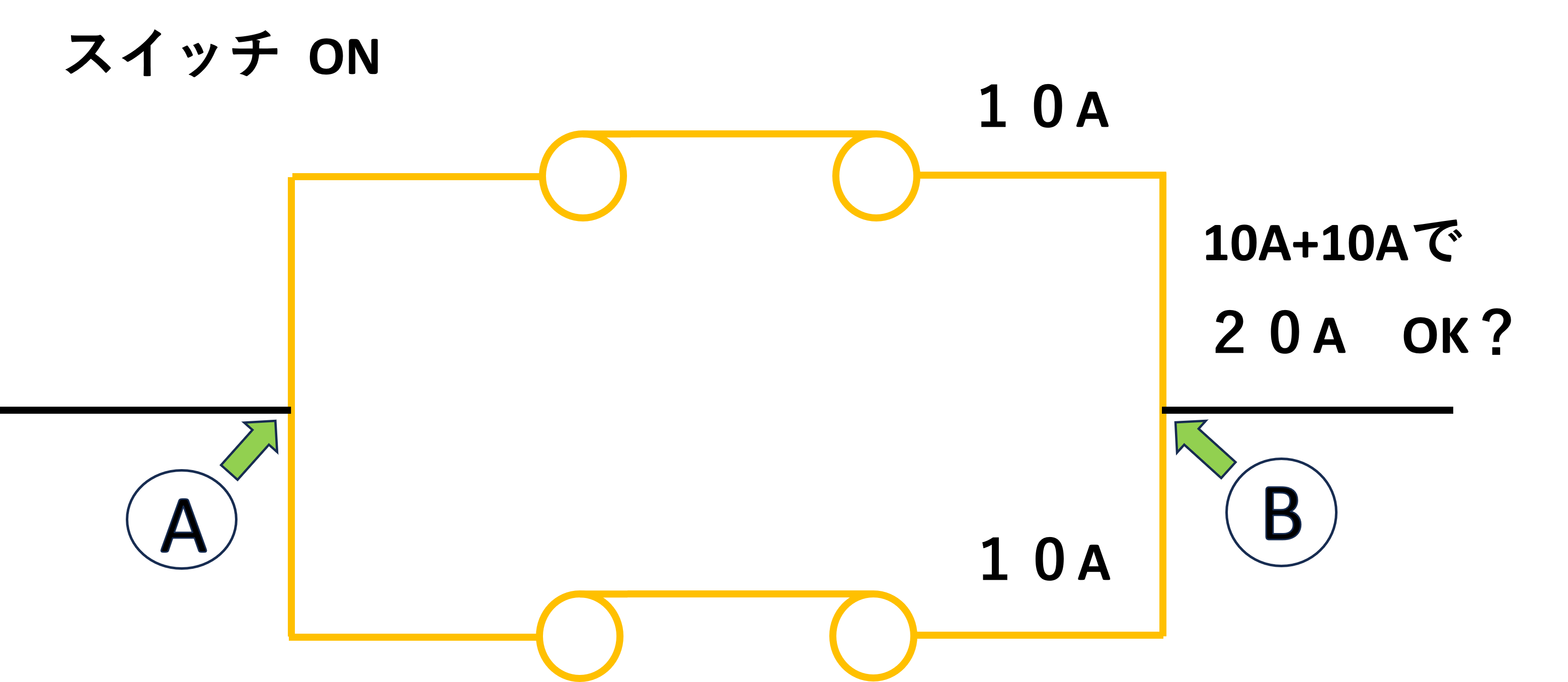
二極並列ON
通常、電路には固有抵抗が小さく、性能-コストバランスの良い銅などを用いますが、抵抗ゼロというわけにはいきません。 食品では、カロリーゼロというものがあったり、なにがしかの条件が付くとカロリーがゼロになる?ようなことを某漫才コンビが言っていたようですが、こと電気に関しては抵抗ゼロというのは、非常に困難ですね。 超電導でもない限り 必ず【抵抗】が存在すると考えるのが普通です。 抵抗に電流が流れれば電圧の降下が起き、同時に電力が熱に変わり、熱による温度上昇が発生します。(定格電流を決める大きな要素の一つにもなっています。)
前置きが長くなっていますが、
10A+10A=20Aの計算で、【ОK】なのでしょうか?
この抵抗の部分を少し細かく見ていくことで何かが出てくるかもしれません。
上の図【二極並列ON】にて、みかん色のところが注目していく部分で、黒線からA点で2分岐して別ルートとなり、またB点で合流して一本の黒線となる間の部分(A-B間)のことです。 そして、どちらのルート上の接点も各々10A流すことの出来る物を使用することとします。 これらのすべての部分に抵抗があります。 抵抗は電線などの導電路、接触したり離れたりする【接点部】(接触部)などそれぞれに存在します。
電線などの導電路は、同じ線を同じ長さにすれば、導体の抵抗は基本的にほぼ同じになります。 【接点部】(接点に限らず、金属の接触部すべて)については導体抵抗のほかに【接触抵抗】がありますが、 これについては、同じ材料を使って同じ構造のものを作っても、ある程度のばらつきが生じることが通常です。 ばらつきは、二個の別の接点ではもちろんのこと一個の接点であっても、閉じたり開いたりするたびに異なる値を示すことがままあります。 また、自己の温度上昇や、開閉による汚れや消耗などから接触抵抗は 変化することがあります。
図のA点からB点に至る道(経路)は、上回り、下回り(仮にこう呼ぶことにします)の2通りあり、A-B間の抵抗がまったく同じであった場合に、10A+10A=20Aの計算は成り立つと考えられます。
上回り、下回りそれぞれが誰かさんと誰かさんのように仲良く10Aづつ受け持てば、それぞれの電流上限値も超えずに合計として20Aが流せることになります。
“仲の良い時” ばかりではありません、、、
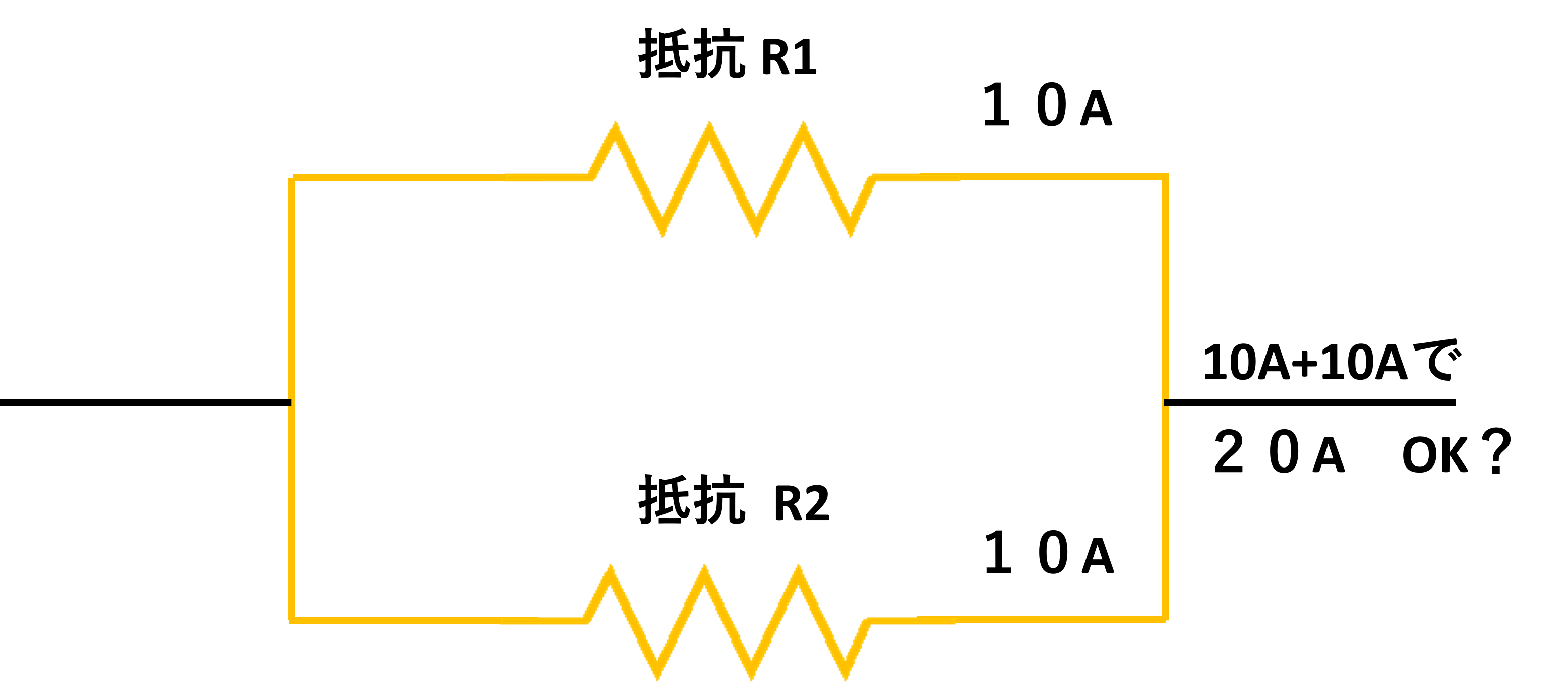
仮想抵抗の二極並列
では、犬と猿のように仲良くなかったら? どうなるでしょうか? 片方が「俺のほうは流させねーよ」、「私のほうはどうぞお気軽にお通り下さい」ということであれば、前者はすなわち、抵抗が大きく、後者は抵抗が小さいと考えを置き換えることができます。 まさに、電流を阻止しようと「抵抗」していることになります。
合計が20Aですから、例えば上回り9A、下回り11Aのようになってしまうとしたら、、、 合計20Aということになるにはなるのですが、それでは20A OK! とはなりません。 それは、下回り側がもともとの許容される電流値である10Aを超えているので、電流が流れすぎとなってしまっています。 合計の20Aは20Aでも、片側が電流超過になってしまっています。 こうなってしまうと、《10A+10A=20A》の《20A》と《9A+11A=20A》の《20A》は合計の数字は同じであってもちょっと違ってきますよね。 ということで、タイトルの【2極を並列に接続したら電流は2倍に?】は、やや危うくなり、2倍というのは無理があるかも知れない、、、雲行きが怪しくなってきましたね。
仲良くないのはどんな時?
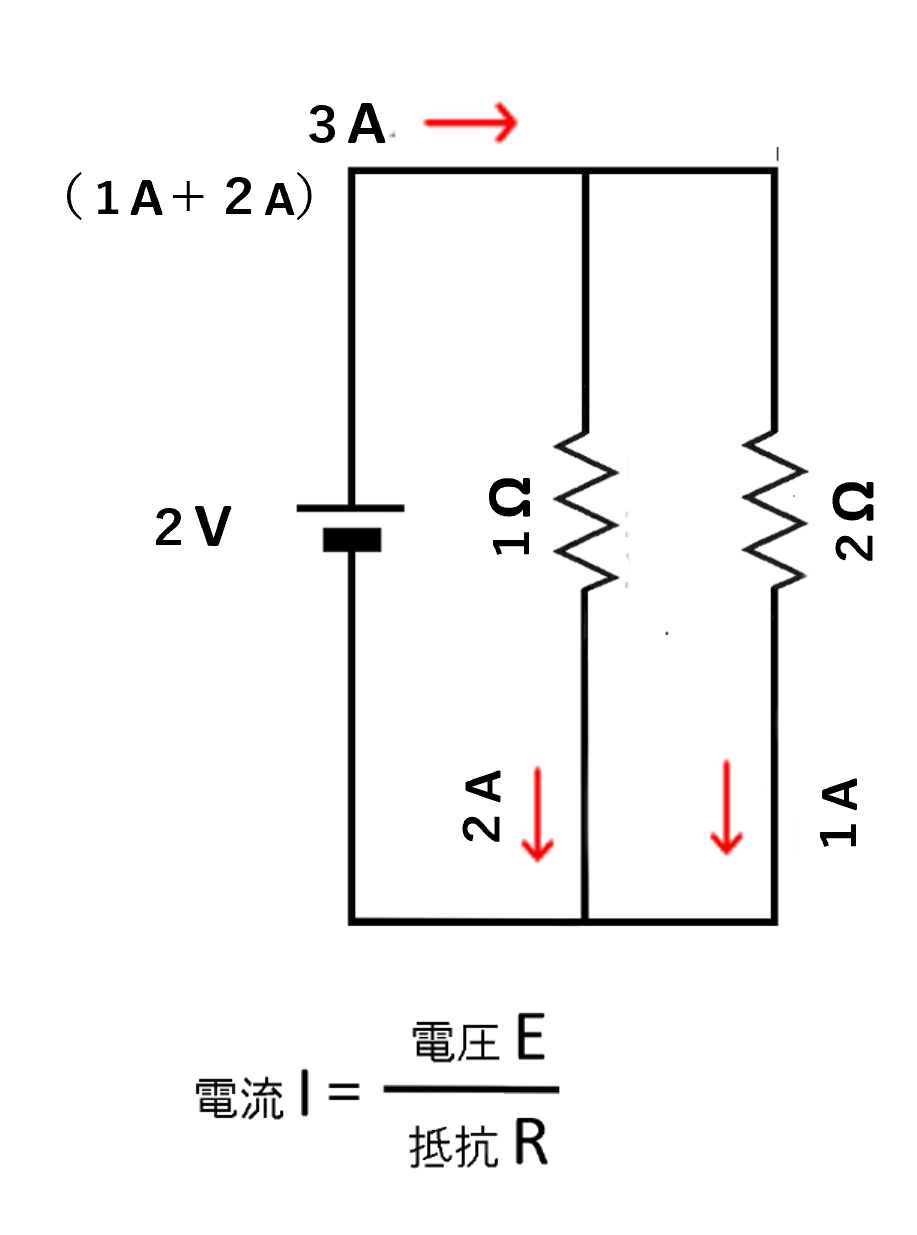
電源と抵抗の単純な回路
それでは、電流はどのようなときに仲良く同じだけ流れてくれないのでしょうか? 当たり前のことですが、電圧が同じである時、抵抗が小さければ電流は大きく、抵抗が大きければ電流は小さくなるので、抵抗値がアンバランスになった場合にそのようになります。 上の例では、接点で話を進めてきましたが、抵抗に置き換えてみましょう。 図では、筆者の好みで、抵抗を旧JIS記号である波線で表しています。 (新JIS記号は長い四角形ですが、電流の流れにくさがなんとなく直感的にわかりやすい、ギザギザのほうが好きで、、、 でこぼこ道を電流という名の車がガタゴトと音をたてながら、一生懸命に走っているような、、、)
結論としては、二つの抵抗の値が同じ時に限り、10A+10A=20A OKとなりますね。 蛇足ですが、抵抗値は配線などを含めた総合的な抵抗値を指します。
ここで、抵抗値がアンバランスな状態では、電流はどのように流れるかを 簡単な例で見てみるために単純・具体化し、回路電圧を2V、抵抗値は、1Ωと2Ω(抵抗値比 1:2)ということにしました。
図【電源と抵抗の単純な回路】
1Ωに流れる電流は、オームの法則から、2V/1Ω=2A、2Ωに流れる電流は、2V/2Ω=1A、合計の電流は、2A+1A=3Aとなります。 つまり、抵抗1Ωには「2A」、抵抗2Ωには「1A」の電流となり、抵抗値の比(1:2)の逆で電流は(2:1)となり【逆比】でそれぞれに電流が流れることになります。 抵抗値の逆比で電流が流れること、抵抗が小さいほうに多くの電流が流れることが具体例で確認できましたので、やや乱暴かもしれませんが具体的なスイッチの話に戻しましょう。 上述のようなスイッチでの接触抵抗ですが、現実的な数値として、一方は5mΩ、もう一方は10mΩなどということがままあります。(抵抗値の比が1:2 の例です) ほかの要素を排除して、接触抵抗のみで考えると、5mΩの側と10mΩの側に流れる電流の和が20Aとなります。 流れる電流は、抵抗の逆比となりますから、20Aの電流を流したとすると、 5mΩの側は、20x10/(5+10)=約13.3A、10mΩの側は、20x5/(5+10)=約6.6A、となります。(単純に20Aを、2:1に分けただけです)
ここで、5mΩの側は、10Aを3.3Aオーバーしていますので、
二極を並列に接続しても10A+10A=20Aとするには無理があるように思えます。
2極を並列に接続しても電流は2倍にならない? 1.5倍とは?

25%引き?
少し省略して端折りますが、どちらの極も10Aを超えないようにすると10A+10A → 15A(目安)となることが考えられます。
20Aを目論んでいたのに、なんと15A? 25%も‘控除?’ いったい20Aにするにはどうしたら、、、良いのでしょうか?
ちなみに15Aにて上記の計算をしてみると、5mΩの側では、15x10/(5+10)=10Aとなることがわかります。 ちゃんとめでたく10Aに収まっています。 念のために、10mΩの側の電流を確かめると、15x5/(5+10)=に5Aとなり、合計で約15Aとなることがわかります。(単純に15Aを、2:1に分けただけです)
上記のことから、2極を並列に接続した場合、単純電流が2倍になると考えると、 場合によっては電流オーバーとなる不都合の生じる可能性があるということになります。 上の例では、
2極を並列に接続した場合、電流は1.5倍まで使用可能と考えられます。 意外と増え方が少ないですね。 しつこいようですが、
抵抗が全く同じ時には、2倍まで使用可能となります。
なお、接触抵抗は、前述のようにスイッチなら接点部、コネクタなら接触部、端子等であれば電線接続部など、金属と金属が接するあらゆるところに存在します。 ちなみに、抵抗値の比が1:2と仮定しましたが、この比が変われば結果も変わってくることは必然となります。 また、接触抵抗は、ずっと同じ値ではなく、スイッチを例にとれば開閉回数を重ねたことによる接点の消耗、形状・表面の荒れ、電流を流したことで発生した熱や微妙な汚れによる接触状態の変化などでも変動することが一般的ですので、1:2と決めてかかると、机上の空論になりかねず注意が必要です。
そう考えると、2極を並列に接続して電流容量を増やすことには、結構な落とし穴があるのかもしれませんね。 しかし、この例のように、接触抵抗の最大が、最小値の2倍以下であれば、単純に流せる電流は、1.5倍と簡易的に考えることで、一応の目安としては役に立つものと思われます。 ちなみに、接触抵抗の最大値が、最小値の3倍であった時にはどうなるかということですが、抵抗値の比は3:1となりますから、抵抗が小さい側には抵抗が大きい側の3倍の電流が流れることになります。 3倍の電流の側が10Aとすると、もう片側はその1/3となるので、10Ax1/3=約3.3Aとなります。 ということで、2極を並列に接続しても、電流は1.3倍程度に収まってしまうことがわかります。 2倍の電流となることを目論んで2極並列としたわりに、1.3倍ではあまり実用的ではないという結果となります。 もともと定格の大きいものを使用するのが賢明かもしれません。 というか、並列に接続して流せる電流を増やすということは、あくまでも応急的な方法として考えるべきかもしれません。 (この記事により、並列接続での使用をお勧めするものではありません。)
2極並列よりもさらに実用的ではないと思われる、3極並列の場合はどのようになるのか?
面白そうなので、次回 “2極を並列に接続したら電流は2倍に?(後編)”で考えてみたいと思います。(現在未掲載)
お読みくださりましてありがとうございます!











